さぁ、
この前の教えを思い出して、今日で一気にCCIをマスターしちゃいましょう !
CCI後編スタートです。
この前の教えを思い出して、今日で一気にCCIをマスターしちゃいましょう !
CCI後編スタートです。

時間おいて脳みそリフレッシュしたんで、バッチ来い!
CCIおさらい

前回までのおさらいになりますが、
CCIは移動平均線乖離率の親戚で、
「今の価格」が「平均的な価格」とどれくらい離れているのかを見ているだけの
指標でしたよね。
CCIは移動平均線乖離率の親戚で、
「今の価格」が「平均的な価格」とどれくらい離れているのかを見ているだけの
指標でしたよね。

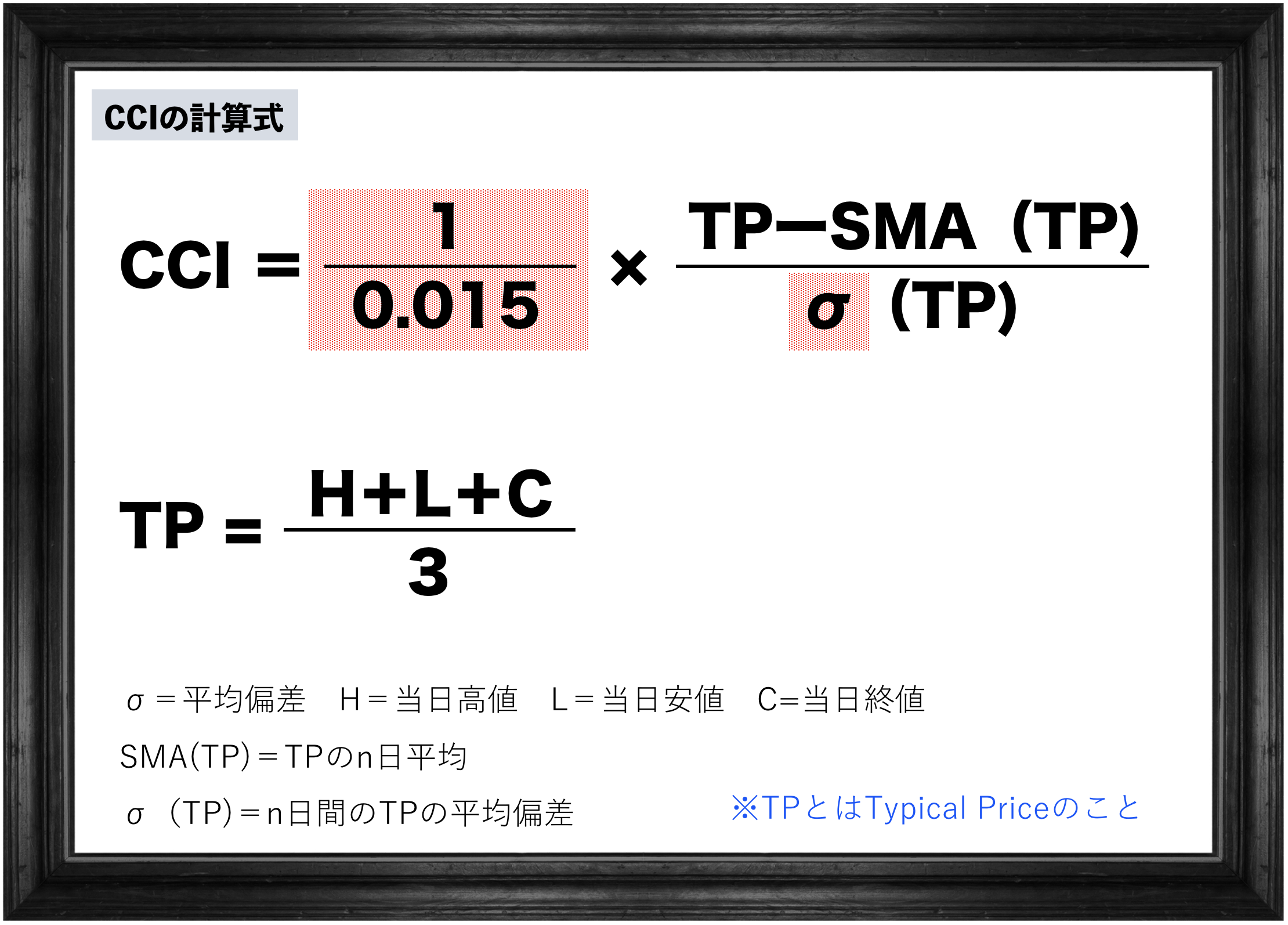
式は複雑でしたが、概要をまとめるとシンプルっすね。

そうそう。そしてアルファベット「TP」は代表値を表しているだけだと。

高値と安値と終値の3つを足して3で割ったものが代表値=TP。

ということは、前回瞬くんが”果樹園マーク”と言っていたこの「σ」と、
なぜ「0.015分の1」なんてヘンテコな数値をかけるのかさえ分かれば
CCIも攻略完了です。
なぜ「0.015分の1」なんてヘンテコな数値をかけるのかさえ分かれば
CCIも攻略完了です。

ここらへんが難しそう…ぐぬぬ。

ここがCCI攻略の天王山ですよ。
でも任せてください。その難所を分かりやすくし、一緒に乗り越えるのが小次郎講師の使命ですから。
でも任せてください。その難所を分かりやすくし、一緒に乗り越えるのが小次郎講師の使命ですから。
平均偏差とは

まずこの記号「σ」、これは「シグマ」と呼びます。

なんか数学の授業でよく聞いたような…

よく見たのは「Σ」こういう記号ですよね?

それだー!!!!サブイボが…!

高校数学の拒否反応出さない!「Σ」も「σ」も同じシグマ。
…って私も文系なので大丈夫ですよ。
…って私も文系なので大丈夫ですよ。

ほ、本当ですか!?

前回も見た、CCIのこの部分と移動平均線乖離率の式とを並べた図。
これを見ると「代表値のσ」と「n日移動平均」がほぼイコールということがわかりますよね。
これを見ると「代表値のσ」と「n日移動平均」がほぼイコールということがわかりますよね。


この2つの式の本質は同じ、って話でしたもんね。

つまりこの「σ」も何かの平均値。
何の平均なのかと言いますと「ある期間の代表値の“平均偏差”」です。
何の平均なのかと言いますと「ある期間の代表値の“平均偏差”」です。

平均…へんさ??

この「偏差」という考え方、統計学に用いられるものなんですよ。
チャート分析もある意味では「過去のパターンから統計を取って未来を予測する」わけですから、似たような性質を持っていますよね。
チャート分析もある意味では「過去のパターンから統計を取って未来を予測する」わけですから、似たような性質を持っていますよね。

言われてみればそうですねぇ。

我々は何も数学や統計学の専門家になろうっていうんじゃありませんから、
専門的に難しい部分まで理解せずとも良いのです。
ですので、平均偏差の概要を知って、それを計算式の中で使いこなせれば上出来。
専門的に難しい部分まで理解せずとも良いのです。
ですので、平均偏差の概要を知って、それを計算式の中で使いこなせれば上出来。

って、そこが難しいんですよ…!

大丈夫です大丈夫です。
同じ偏差を用いた考え方を使用するのが、あの有名なテクニカル指標「ボリンジャーバンド」。瞬くんも知ってますよね?
同じ偏差を用いた考え方を使用するのが、あの有名なテクニカル指標「ボリンジャーバンド」。瞬くんも知ってますよね?

はい!確かに知ってますとも。

ボリンジャーバンドでは「標準偏差」という考え方を使うんですが、
それは今度ボリンジャーバンドの解説をする時に詳しくお教えするとして、今日はまず「平均偏差」。
両者とも考え方は同じですが、
標準偏差よりも平均偏差の方が簡単だと思います。
という意味で、良かったですね!
それは今度ボリンジャーバンドの解説をする時に詳しくお教えするとして、今日はまず「平均偏差」。
両者とも考え方は同じですが、
標準偏差よりも平均偏差の方が簡単だと思います。
という意味で、良かったですね!

(まだ概要が分かってないので、手放しでは喜べない…)

これら2つの考え方に共通してるのは「価格変動の大きさ」
つまり「ボラティリティ」を表すものだと、まずは思ってください。
つまり「ボラティリティ」を表すものだと、まずは思ってください。

了解です。まずはそこから。

では、平均偏差の計算の仕方から見ていきましょう。


絶対値ってなんでしたっけ…?昔学校で習ったような…

言葉で説明すると、
「数直線上のある点と原点との距離」と言えますが、
分かりづらいので図で見てみましょう。
「数直線上のある点と原点との距離」と言えますが、
分かりづらいので図で見てみましょう。
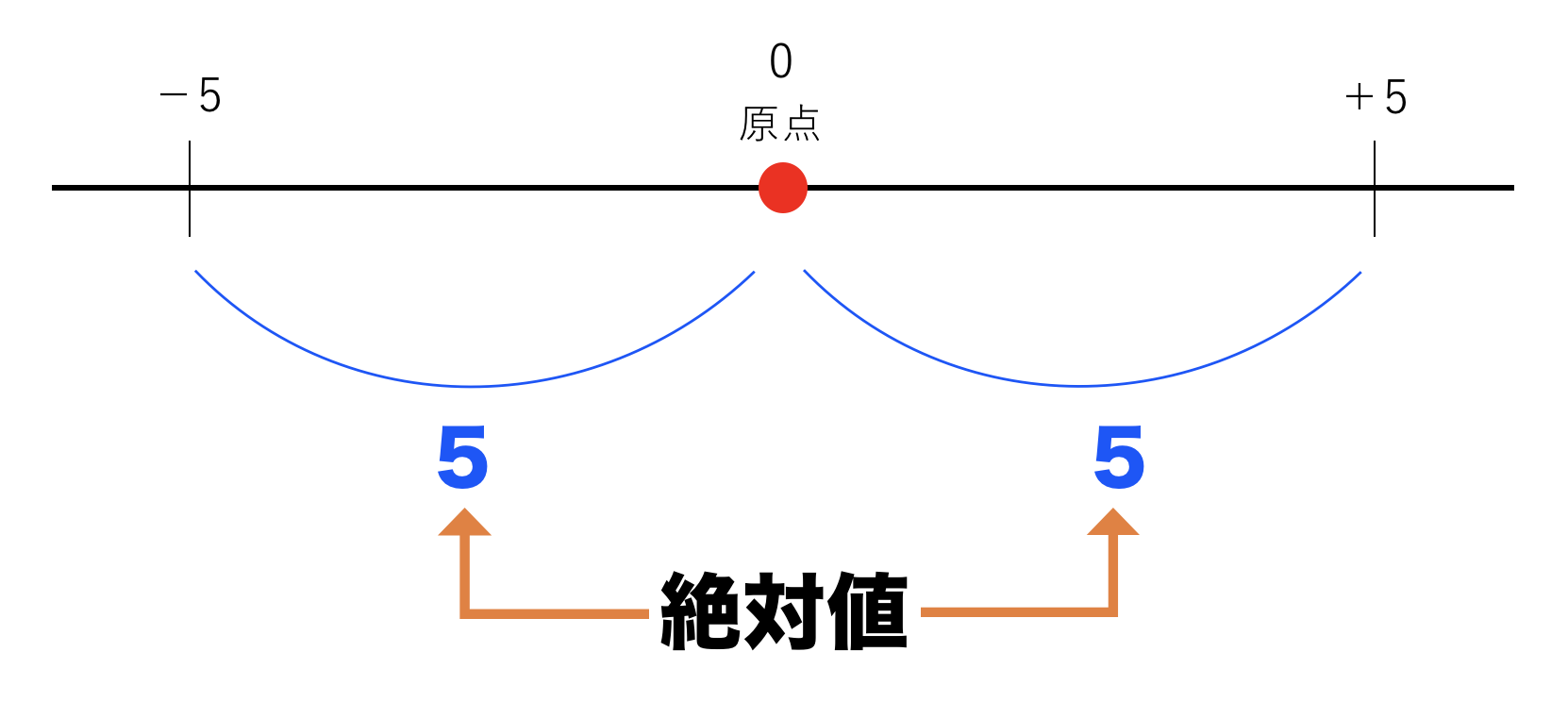

この場合だと、どちらも中心(原点)から5ずつ離れているので、
−5の地点も+5の地点も距離は「5」ということになりますね。
−5の地点も+5の地点も距離は「5」ということになりますね。

距離にマイナスはないですもんね!

分かりやすく言えば
「基本となる場所からどれだけ離れてるか」
という意味です。
「基本となる場所からどれだけ離れてるか」
という意味です。

あ!だから絶対値は正の値にしかならないとか数学の先生に言われてたの、思い出しました!

それを上に出した平均偏差の計算の仕方に当てはめると、
絶対値で出した、各データと平均値(原点)の差(②)を、
さらに平均する(③)、ということです。
絶対値で出した、各データと平均値(原点)の差(②)を、
さらに平均する(③)、ということです。

ふむふむ。平均化の作業を2回と。

各データと平均値の差のことを「偏差」と言いますので、
「偏差を平均したもの」と言い換えることもできますね。
「偏差を平均したもの」と言い換えることもできますね。

それで「平均偏差」か!

そもそも受験でよく聞くような”偏差値”も、
あなたは平均点とどれだけ離れてますよ、ってことを教えてくれるものさしですからね。
あなたは平均点とどれだけ離れてますよ、ってことを教えてくれるものさしですからね。

偏差値50が平均点。
そう言われると身近に感じるなぁ。
そう言われると身近に感じるなぁ。

じゃあ、この平均偏差をテストの点数で説明してみましょうか。
100点満点のテストの平均点が60点だったとしましょう。
そしてあるクラスの子らの点数が以下の通り。
100点満点のテストの平均点が60点だったとしましょう。
そしてあるクラスの子らの点数が以下の通り。
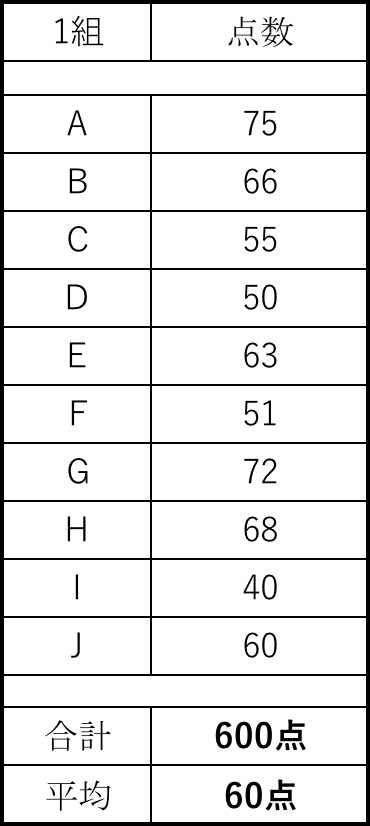

生徒数が少ない山の上の学校みたいだ…

分かりやすくする為に人数減らしているだけなので、余計なこと言わない!!

は、はいっす!!

この各自の点数と平均点との差が「偏差」。
でも絶対値、正の数で表したいので、平均点との”距離”と考えるとこう。
でも絶対値、正の数で表したいので、平均点との”距離”と考えるとこう。
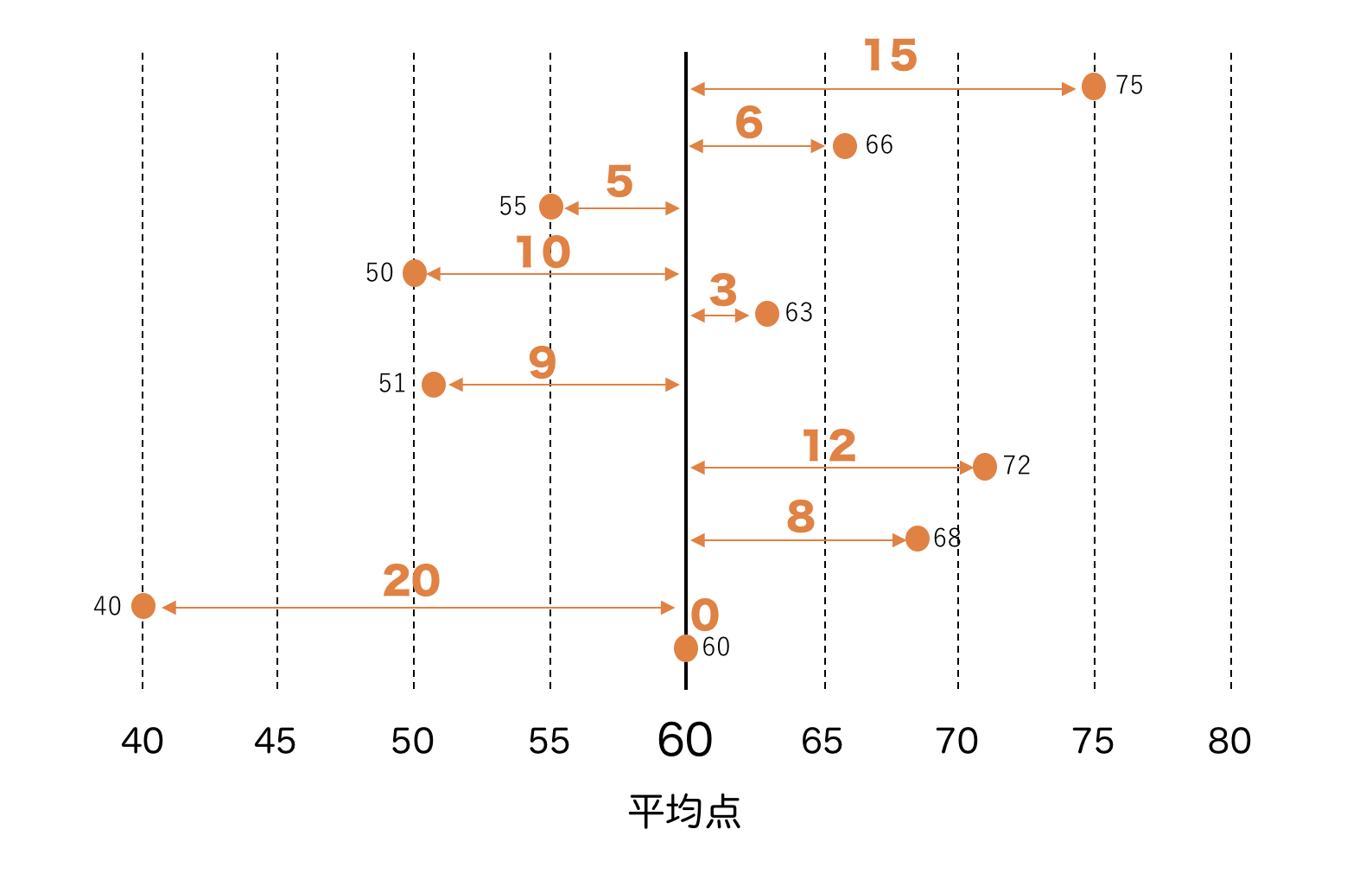

で、この距離の(偏差の)平均を求めると、それが「平均偏差」になると。

そうです!
よって先ほどの点数表に平均偏差を付け加えると、こういうことになります。
よって先ほどの点数表に平均偏差を付け加えると、こういうことになります。
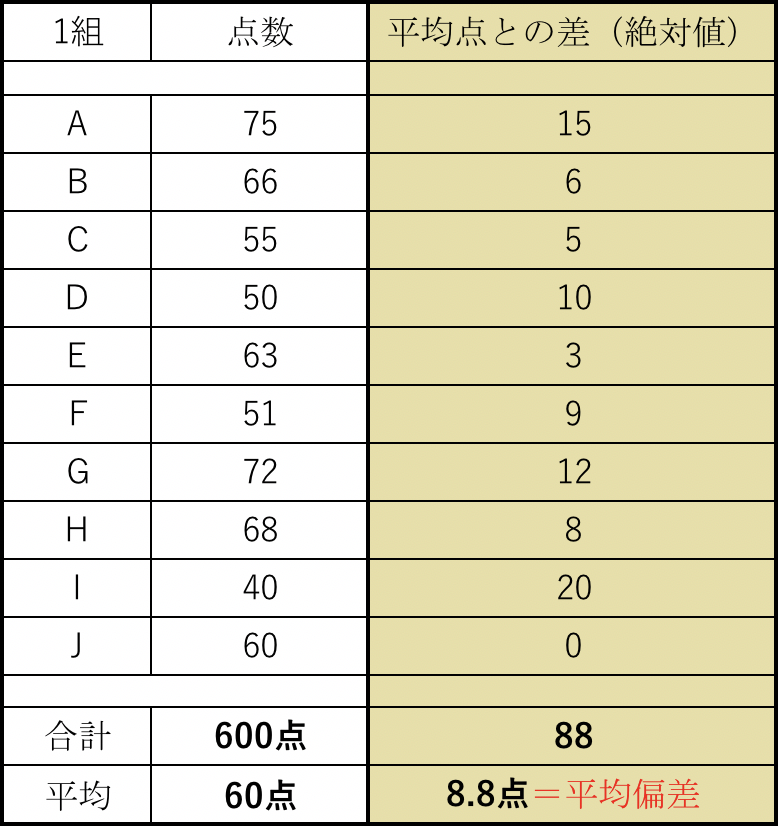

このクラスの生徒たちは、平均点と平均的に8.8点離れてるってことが分かるんですね!

単語が重複しちゃってますが、そういうことです。
じゃあさっきのものを1組として、2組はこういう成績でした。
じゃあさっきのものを1組として、2組はこういう成績でした。
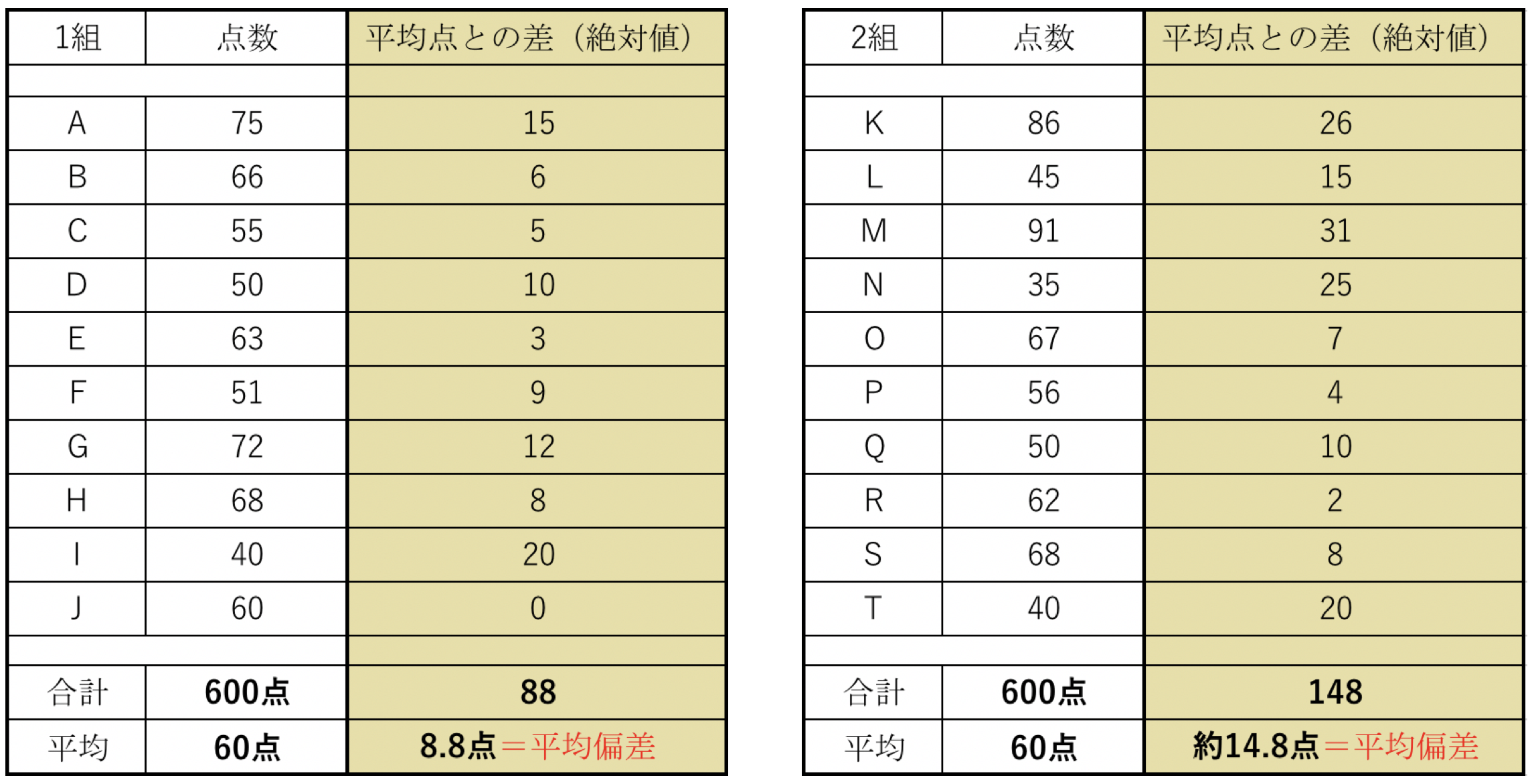

あれ…?
平均点は一緒なのに、平均偏差は2組の方が大きい…。なんでだろ?
平均点は一緒なのに、平均偏差は2組の方が大きい…。なんでだろ?

1組は最低点40点と最高点75点に対して、2組の方は最低35点と最高91点で、点数のバラツキの幅が広いですよね?

確かに点数の良い子と悪い子の振れ幅が大きい。

そういう場合、平均は同じでも「平均偏差」は大きくなるんです!
これが価格に当てはめて言うと「ボラティリティの高い状態」!
これが価格に当てはめて言うと「ボラティリティの高い状態」!

やっとチャートに話が戻ってきた!!

つまりこの「σ」は平均偏差を表しているので、
ある期間の値動きの幅が大きいんですか、小さいんですかということを表しているに過ぎないんです!
ある期間の値動きの幅が大きいんですか、小さいんですかということを表しているに過ぎないんです!
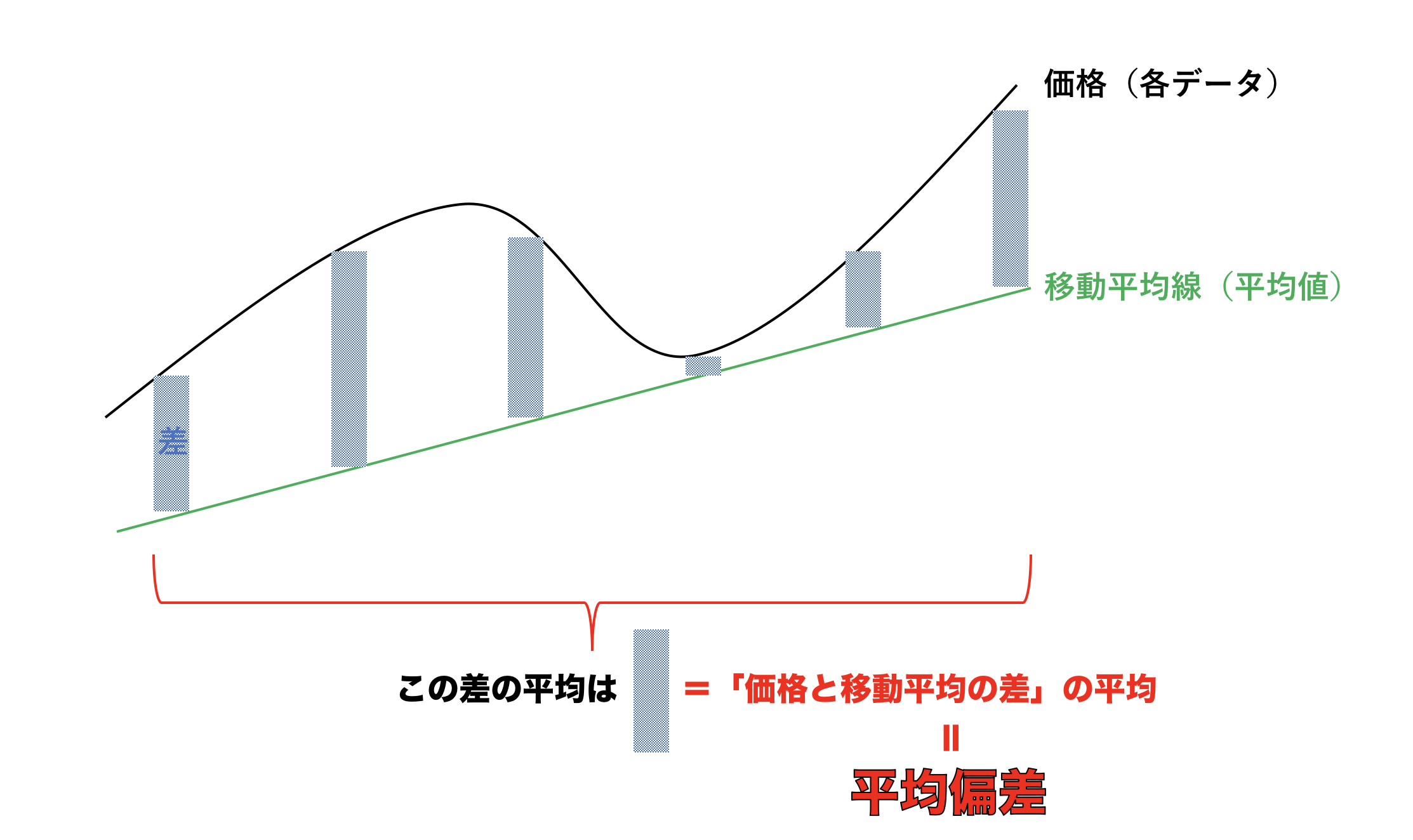

平均値を見てるので、やっぱり移動平均線乖離率の方の「n日移動平均」の部分と考え方は一緒なんですね。
あ、ところで平均偏差の”ある期間”って何日間の値幅を見るんですか?
あ、ところで平均偏差の”ある期間”って何日間の値幅を見るんですか?

CCIの場合は移動平均線乖離率と同じく14がよく使われますね。

まとめると
「今の価格と14日移動平均の価格との差、これがどのくらい差があるのが平均的な状態か。」を、この平均偏差「σ」で表しているんですね。
「今の価格と14日移動平均の価格との差、これがどのくらい差があるのが平均的な状態か。」を、この平均偏差「σ」で表しているんですね。
1÷0.015の意味

それでは満を持して、
最後の鬼門のココの話をしましょう。
最後の鬼門のココの話をしましょう。
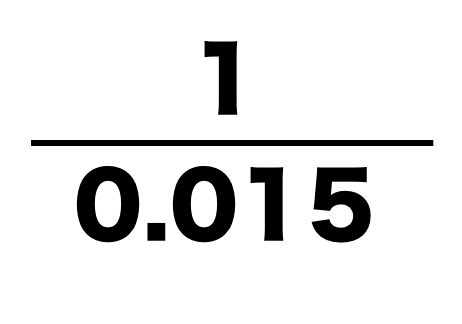

と、その前に前回したこの会話の部分を覚えていますか?
(ほわほわほわ〜ん)
(ほわほわほわ〜ん)


効果音つけて画面キャプチャー見せなくても覚えてますよ…!

記憶力を試しました 笑
というのは置いといて、この部分をもう少し掘り下げて考えると
「数値が100を超えると売りサイン」とはどういうことか。
というのは置いといて、この部分をもう少し掘り下げて考えると
「数値が100を超えると売りサイン」とはどういうことか。

100以上になると平均値と離れすぎですよ!ってことですよね。

そう、意味合いはそうなんです。
それをCCIで計算式に表すとこうです。
それをCCIで計算式に表すとこうです。


代表値とか取っ払って、式を簡略化してますね。

で、数学的な話になりますが、
この式は書き換えるとイコールこうです
この式は書き換えるとイコールこうです


分数のかけ算は分子同士、分母同士をかけるというアレだ。

そして確認ですが、不等号の右と左に同じ正の数をかけても
不等号は変わらない、ということは知ってますよね?
不等号は変わらない、ということは知ってますよね?

3>2の左右に10をかけても不等号は変わらず式は成立するって意味ですよね?

おぉ!よく分かってるじゃないですか!

これが僕の算数のギリギリです 笑

では、それに従って式を解き進めて行ってみましょう。
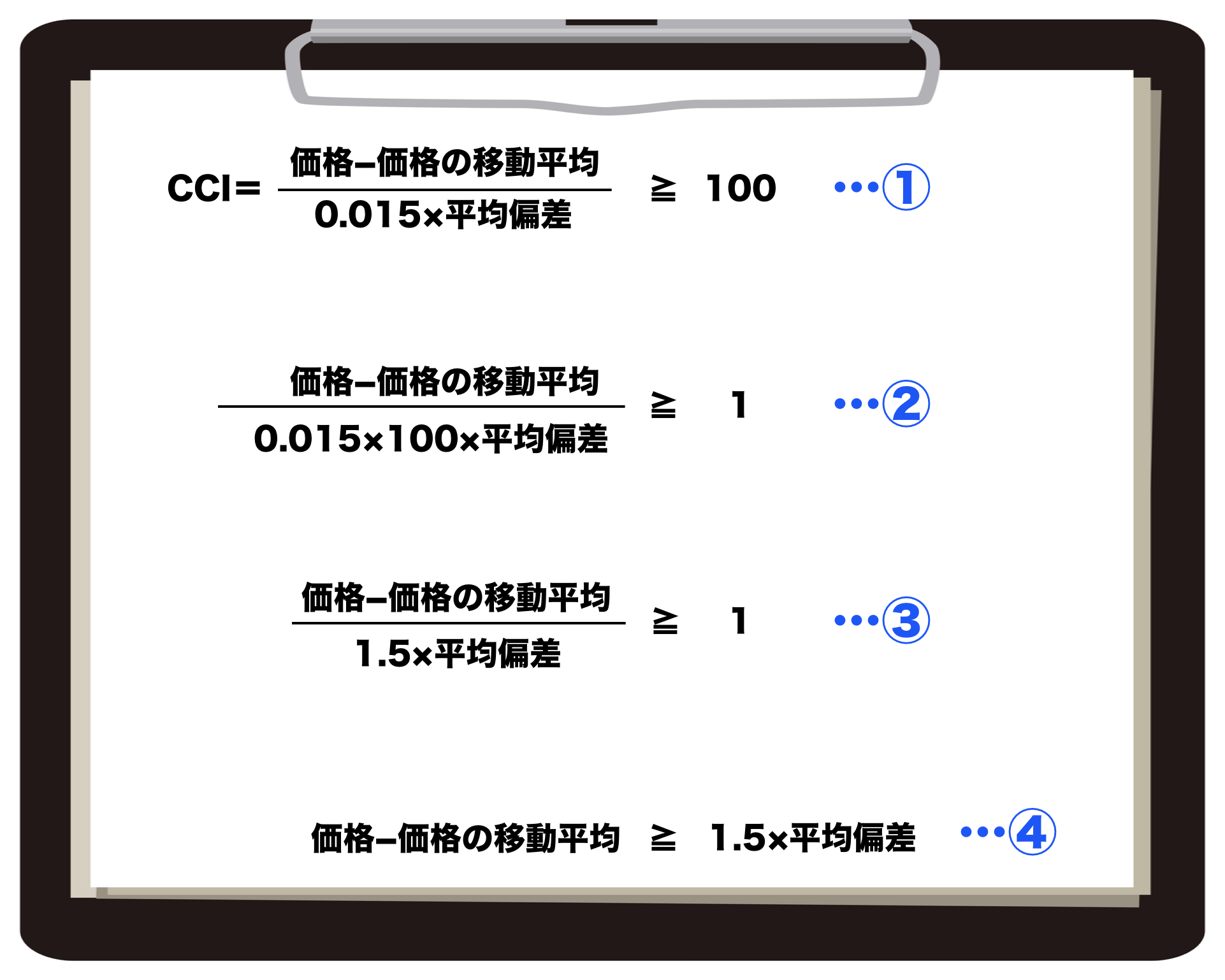

① の部分はCCIが100を超えることが1つのサインですよ、という意味。
② は式を簡略化するために不等号の左右を100で割ったもの(100分の1を掛けたもの)。
③ で0.015×100を計算し
④ は分母があると分かりづらいので、分母を消すために左右に「1.5×平均偏差」をかけたもの
② は式を簡略化するために不等号の左右を100で割ったもの(100分の1を掛けたもの)。
③ で0.015×100を計算し
④ は分母があると分かりづらいので、分母を消すために左右に「1.5×平均偏差」をかけたもの

おぉ!だいぶスッキリしましたね!

最終的な式がこちら。


いいですか瞬くん。
この式から分かることは
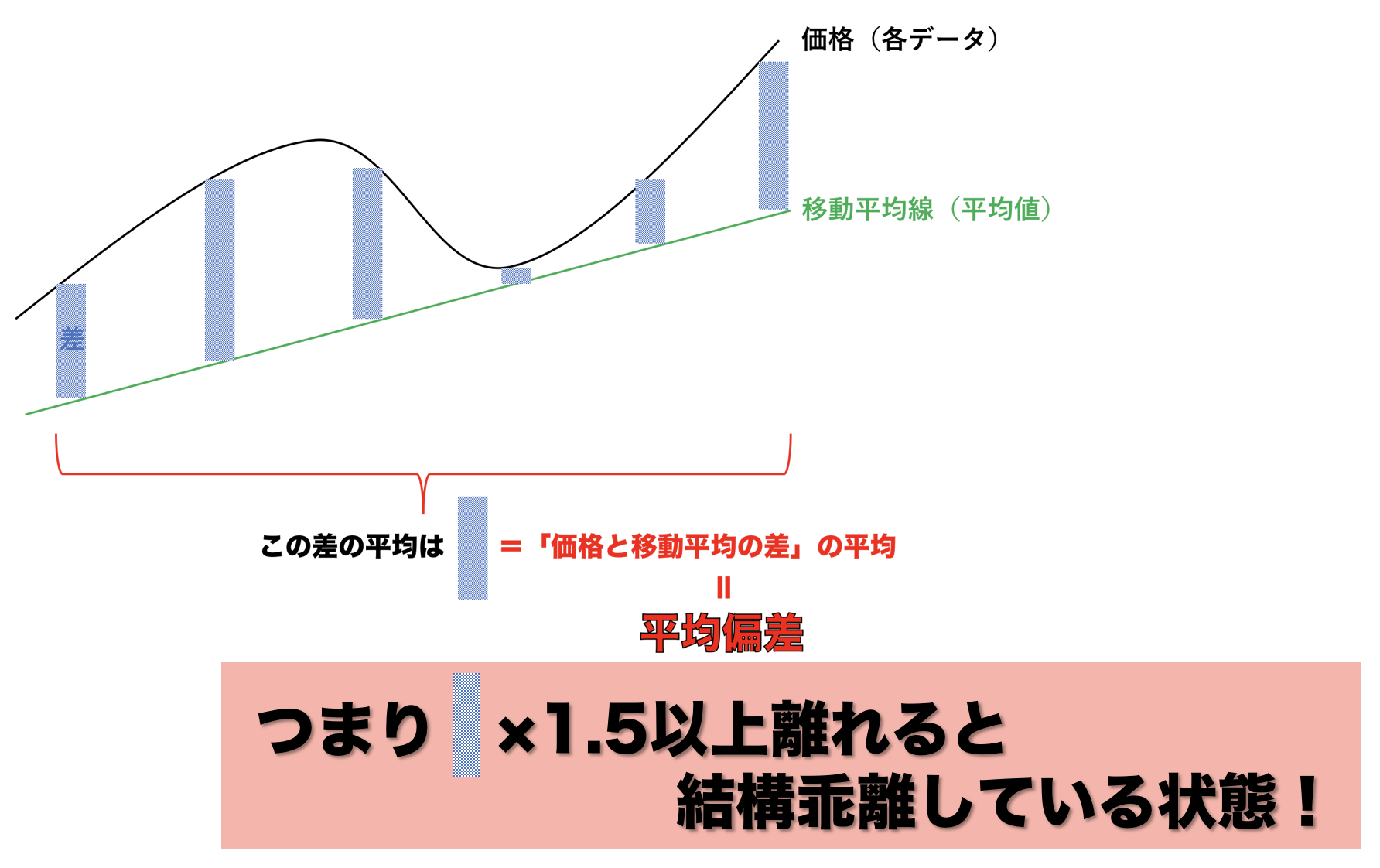
CCIが100を超えるということは、価格と移動平均線の差が、平均偏差(つまり価格と移動平均線の差の平均)の1.5倍を超えたという意味なんです。
この式から分かることは
CCIが100を超えるということは、価格と移動平均線の差が、平均偏差(つまり価格と移動平均線の差の平均)の1.5倍を超えたという意味なんです。

そうか。
例えばある期間の平均偏差が100円、つまり価格と移動平均の差=100円が通常運転の状態で、それが1.5倍の150円離れてたら、なかなか離れてるな!と思いますもんね。
例えばある期間の平均偏差が100円、つまり価格と移動平均の差=100円が通常運転の状態で、それが1.5倍の150円離れてたら、なかなか離れてるな!と思いますもんね。

そう考えるのがCCI。
言い換えると、
平均偏差の1.5倍上に価格が離れること=CCIが100を越えるということ
平均偏差の1.5倍下に離れることが=CCIが-100を越えるということ。
言い換えると、
平均偏差の1.5倍上に価格が離れること=CCIが100を越えるということ
平均偏差の1.5倍下に離れることが=CCIが-100を越えるということ。
本当の買いシグナルと売りシグナル

でも、さっきの画面キャプチャーの会話を思い出すと、
100を超えてもそれだけを売りサインとしてはいけないんですよね?
100を超えてもそれだけを売りサインとしてはいけないんですよね?

価格と移動平均との差が、通常時の1.5倍というのは
トレンドが発生していたら十分あり得る数値。
そこで売りを仕掛けてもまだまだ価格は上がっていくかもしれません。
トレンドが発生していたら十分あり得る数値。
そこで売りを仕掛けてもまだまだ価格は上がっていくかもしれません。

じゃあ流石に200や−200を超えたら買われ過ぎ売られすぎっすよね!?

200を超えるということは、通常時の乖離率に対して現在は3倍になっているということです。

200なのに3倍…?なんでだ?

先ほどの式は100を基準に考えていましたから、100の部分のそこの数字にXを代入してみましょう。
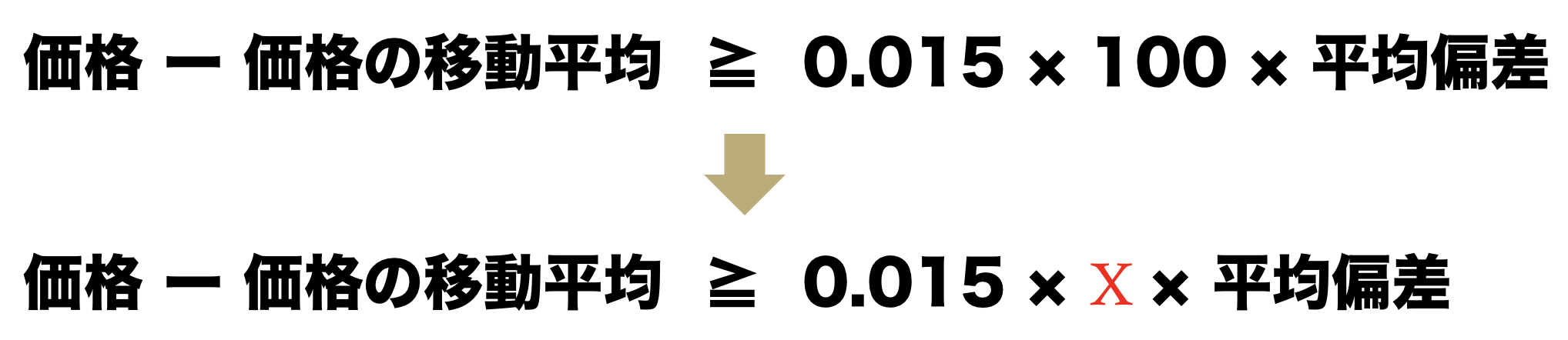

このXの部分が200だと…えーと。

0.015×200×平均偏差で答えは「3×平均偏差」になります。

ホントだ3倍だ!
確かに3倍も離れてたらヤバイっすよね。
確かに3倍も離れてたらヤバイっすよね。

ということで理論上はCCIは200、300超えもあり得ますが
それだけ通常との乖離が激しいレアな状態と考えてください。
それだけ通常との乖離が激しいレアな状態と考えてください。

でも、それがレアな珍しい状態ってことは、
トレンドの勢いが弱まってきたら通常の乖離状態に戻っていく、と。
トレンドの勢いが弱まってきたら通常の乖離状態に戻っていく、と。

そう、そこの考え方が大事なんです!
離れ過ぎが戻ってきたら、トレンドの勢いがなくなってるという意味ですから、トレンドの終焉が近づいていることの予兆でもあります。
そうすると今度は反対のトレンドが発生するかもしれない、ということで逆の売買を仕掛けていく。
離れ過ぎが戻ってきたら、トレンドの勢いがなくなってるという意味ですから、トレンドの終焉が近づいていることの予兆でもあります。
そうすると今度は反対のトレンドが発生するかもしれない、ということで逆の売買を仕掛けていく。


これがCCIの売買シグナルとその根拠なんですねぇ。

CCIは移動平均線乖離率を進化させたもの、という説明がようやく分かったでしょう?

合点がいきました!
CCIは移動平均線乖離率に”代表値”と”平均偏差”の考え方をプラスしたものなんですね。
CCIは移動平均線乖離率に”代表値”と”平均偏差”の考え方をプラスしたものなんですね。
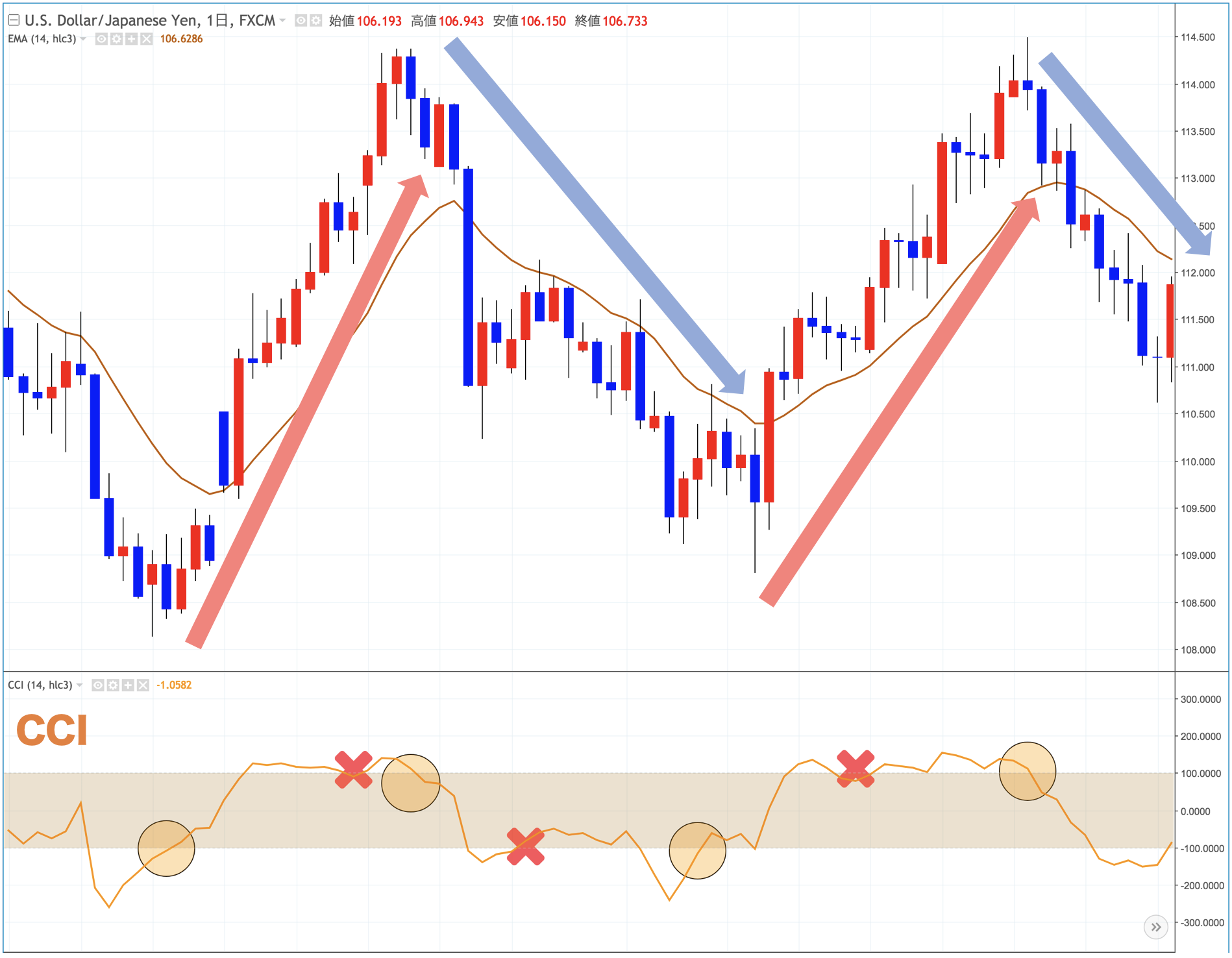

まぁまぁダマシも多いのでCCIだけを売買の根拠とするのではなく、他の指標との組み合わせで使うのがオススメですが、
ここまでCCIを詳しく説明している解説は他にありませんよ 笑
一度では分からないことも繰り返し考えていけば、いつか必ず理解できるようになりますので、CCIの今回と前回の記事を繰り返し復習してみてくださいね。
ここまでCCIを詳しく説明している解説は他にありませんよ 笑
一度では分からないことも繰り返し考えていけば、いつか必ず理解できるようになりますので、CCIの今回と前回の記事を繰り返し復習してみてくださいね。

まだ頭こんがらがってますが、決して諦めないっす!
…でも不思議と小次郎講師と一緒に順を追って見ていくとすんなり理解できるんすよね。
…でも不思議と小次郎講師と一緒に順を追って見ていくとすんなり理解できるんすよね。

おぉ、それは嬉しいですね。

後で一人で考えると途端に分かんなくなってしまうんですけど。

勉強というものは往々にしてそうですが、
自分の頭でしっかり考えるその瞬間に、教わったことが身についていくんですよ。
自分の頭でしっかり考えるその瞬間に、教わったことが身についていくんですよ。

でも、それだと時間かかってしまうので、手っ取り早く小次郎講師レンタルしてもいいですか?

なんと意志薄弱…!!

一家に一台、小次郎講師。

昭和の家のテレビか!
おしまい