梅がそろそろ咲き始めましたねぇ。風流風流。

もうそんな季節ですねぇ。

こういう時こそ日本人で良かったと思いますよ。

最近、おにぎりでも「梅干しが苦手」と言う人が増えてますが、瞬くんは平気ですか?

大好きっすよ!昔からおばあちゃんがよく食べさせてくれて。
あの酸味は疲れが吹き飛ぶ感じしますもんね。
あの酸味は疲れが吹き飛ぶ感じしますもんね。

好き嫌いがなくて結構結構。

あ〜、梅干しのこと考えただけで、口の奥がきゅーって酸っぱくなって唾液出て来ますよね。不思議。

それは過去の経験を基にした、一種の条件反射なんですよ。

“パブロフの犬”的なですか?

そうです。その記憶が副交感神経を刺激して唾液の分泌を促すのです。
「梅を望んで渇きを止む」なんていう、古くは三国志の時代に生まれた中国のことわざもあるくらいですから。
「梅を望んで渇きを止む」なんていう、古くは三国志の時代に生まれた中国のことわざもあるくらいですから。

へぇ!今も昔も変わらずなんですね。

また、その考えて出て来ただけの唾液にも、各種のホルモンや消化酵素も含まれていて、身体にはとても良いらしいですよ。

小次郎講師、博識ですねぇ!

私も、良い形のチャートを見ると思わず”垂涎”してしまうもので。

職業病かもしれませんが、確かにエッジのある”オイシイ”チャートを見ると
我々ヨダレ出そうになりますもんね 笑
我々ヨダレ出そうになりますもんね 笑
CCIって?

今回はオシレーター系の「CCI」というテクニカル指標を勉強していきましょう。

この指標も買いや売りの”オイシイ”ところを教えてくれるんですね!?ハッハッ!

そんなワンコみたいに反射で食いつくんじゃありません!
この指標もちゃんと学ばないと、どこが”オイシイ”ところか教えてくれませんよ!
この指標もちゃんと学ばないと、どこが”オイシイ”ところか教えてくれませんよ!

そうでした…!概要だけで食いついちゃダメだダメだ。

「CCI」とはCommodity Channel Indexの略。
1980年にアメリカの投資家ドナルド・ランバート氏によって開発された
オシレーター系のテクニカル指標です。直訳すると「商品チャネル指数」。
1980年にアメリカの投資家ドナルド・ランバート氏によって開発された
オシレーター系のテクニカル指標です。直訳すると「商品チャネル指数」。

チャネル、って「チャネルライン」とかのチャネルですか?

そうそう。そもそも「Channel」とはテレビのチャンネルと同じ意味で、
経路、水路、溝などという意味があります。
チャートで言うとトレンドラインの反対側に平行に描かれる
このラインを含めチャネルラインですから、
確かに真っ直ぐな”水路” っぽいですよね。
経路、水路、溝などという意味があります。
チャートで言うとトレンドラインの反対側に平行に描かれる
このラインを含めチャネルラインですから、
確かに真っ直ぐな”水路” っぽいですよね。
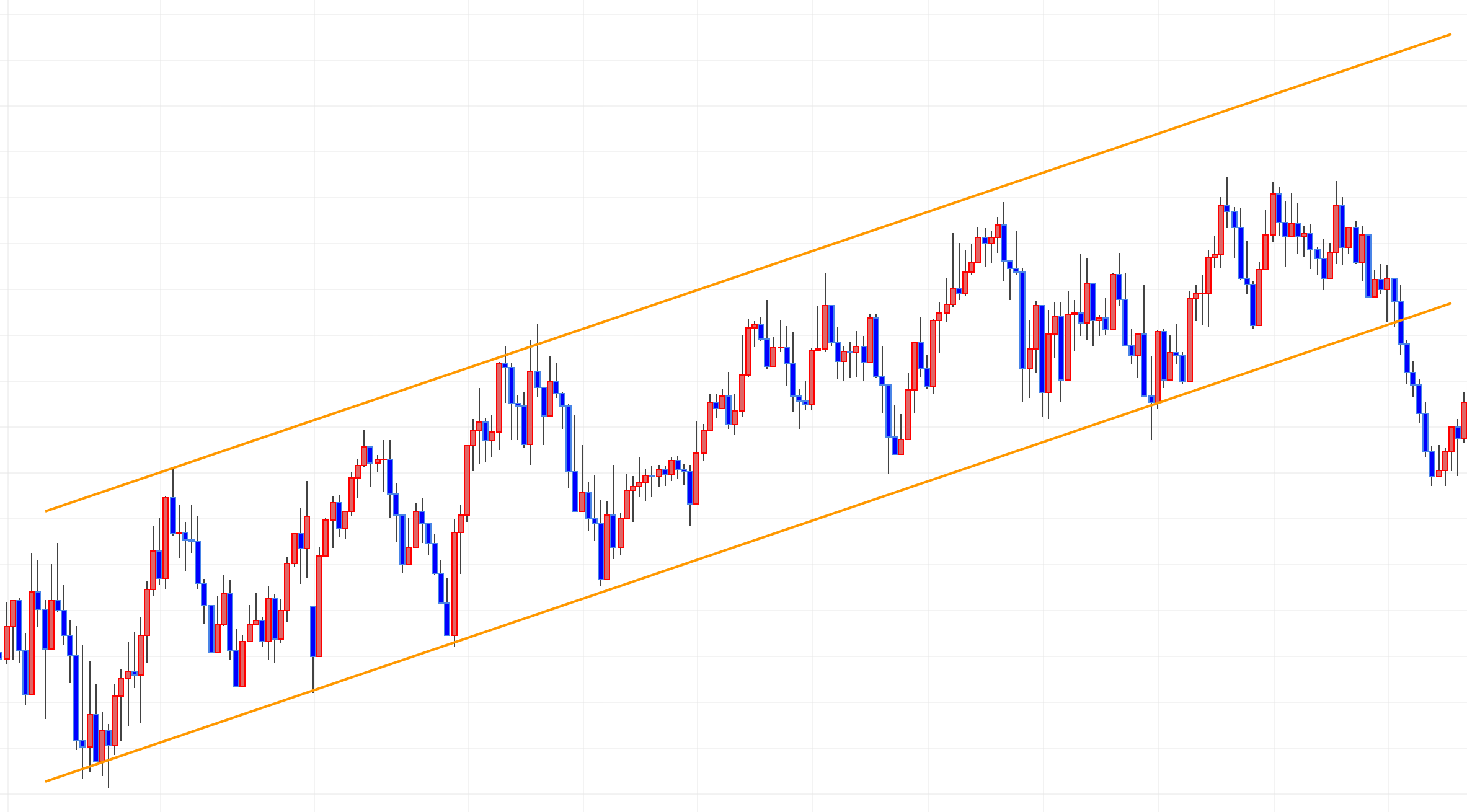

本当だ。流れが分かりやすいっす。

ランバートさんは元々商品市場の季節性や需給サイクルの
始まりや終了を読み取る為にこの指標を作り出したそうです。
始まりや終了を読み取る為にこの指標を作り出したそうです。

金とか穀物とかの商品市場で使われてたんすね!

作った時はそうでしたが、今ではFXや株式にも広く使われています。
チャートがあるものは同じ考え方が出来ますから。
チャートがあるものは同じ考え方が出来ますから。

これもオシレーター系のテクニカル指標ってことは
また−100から+100の間で動くんですか?今まで習ったRSIやストキャスのように。
また−100から+100の間で動くんですか?今まで習ったRSIやストキャスのように。

お!知識の蓄積がキチンと積み重なっているようで嬉しいですね。

えっへん!

理由は後でしっかりと説明しますが、CCIは理論的に100を超えていくらでもつける可能性があります。
ただ、大体は大きくても−200〜+200の間ですけどね。
ただ、大体は大きくても−200〜+200の間ですけどね。

結構振れ幅あるんですね!

これがCCIを付けたチャート。
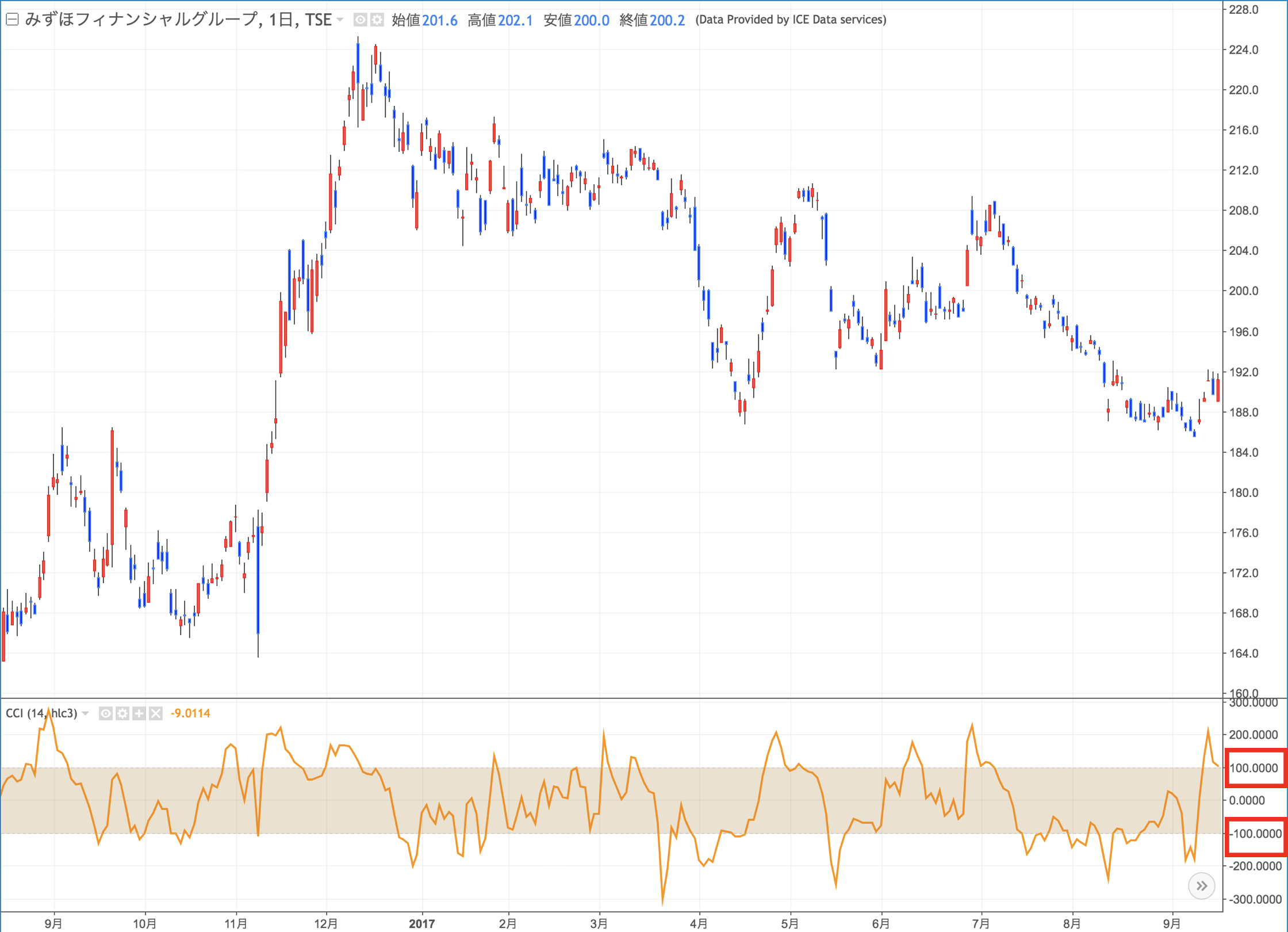

あら、本当に100を超えてらっしゃる。

そして、一般的には数値が100を超えると買われ過ぎだから売りサイン、
−100を下回ると売られ過ぎだから買いサインと言われますが…
−100を下回ると売られ過ぎだから買いサインと言われますが…

そういうのを鵜呑みにしちゃダメってことですね!?(にやり)

そこまでもう分かってるとは!

いつもこのパターンですから、いくら僕だって分かって来ますよそりゃ 笑

確かにそのパターンですもんねいつも…!
これは失礼いたしました。
これは失礼いたしました。

へへ、僕だって成長してるんすよ。

じゃあ、そんな頼もしい瞬くんに、
まずはCCIの計算式からお見せしましょう。
まずはCCIの計算式からお見せしましょう。
CCIの計算式を覚える

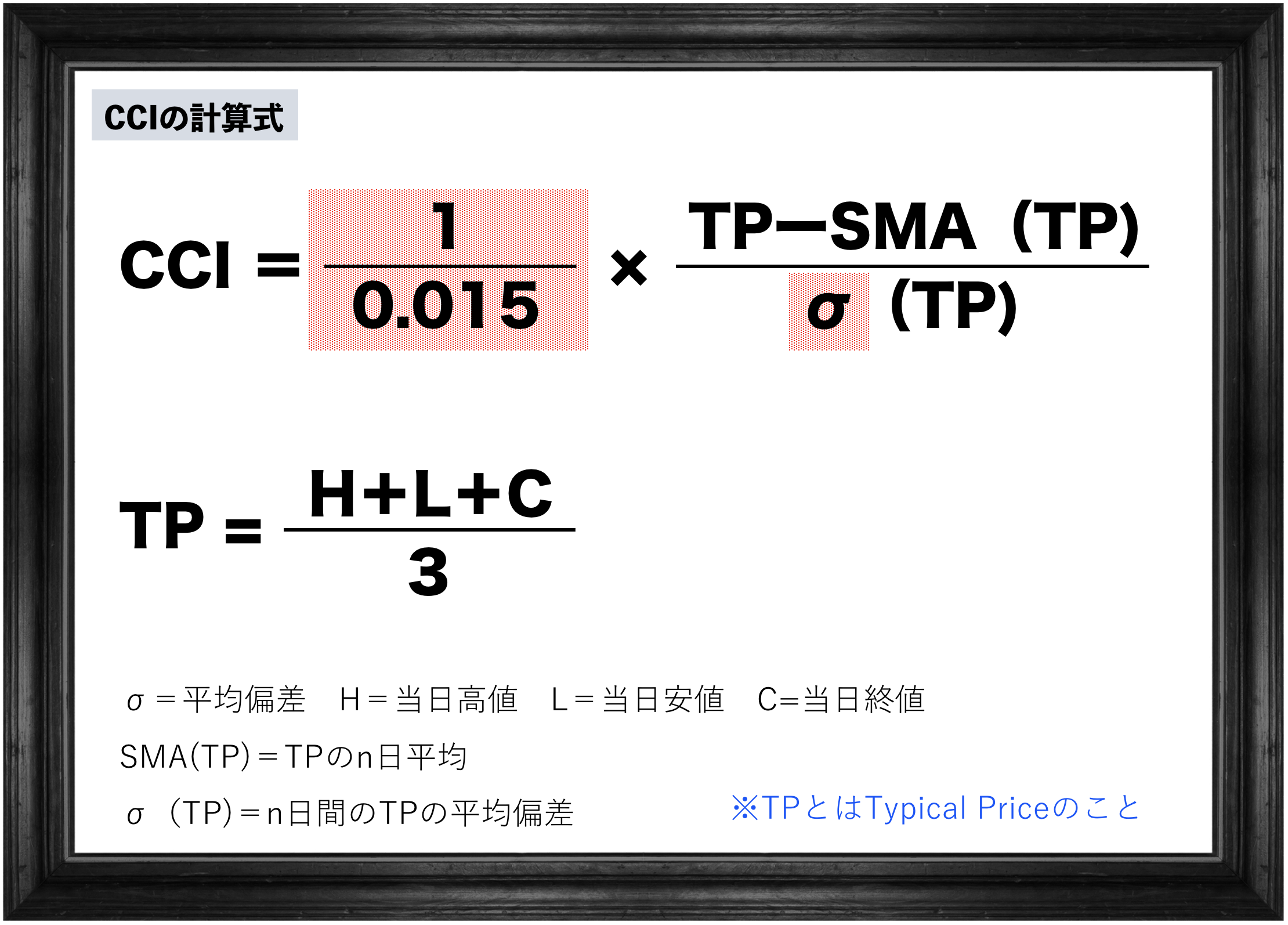
CCIの計算式は以下の通り
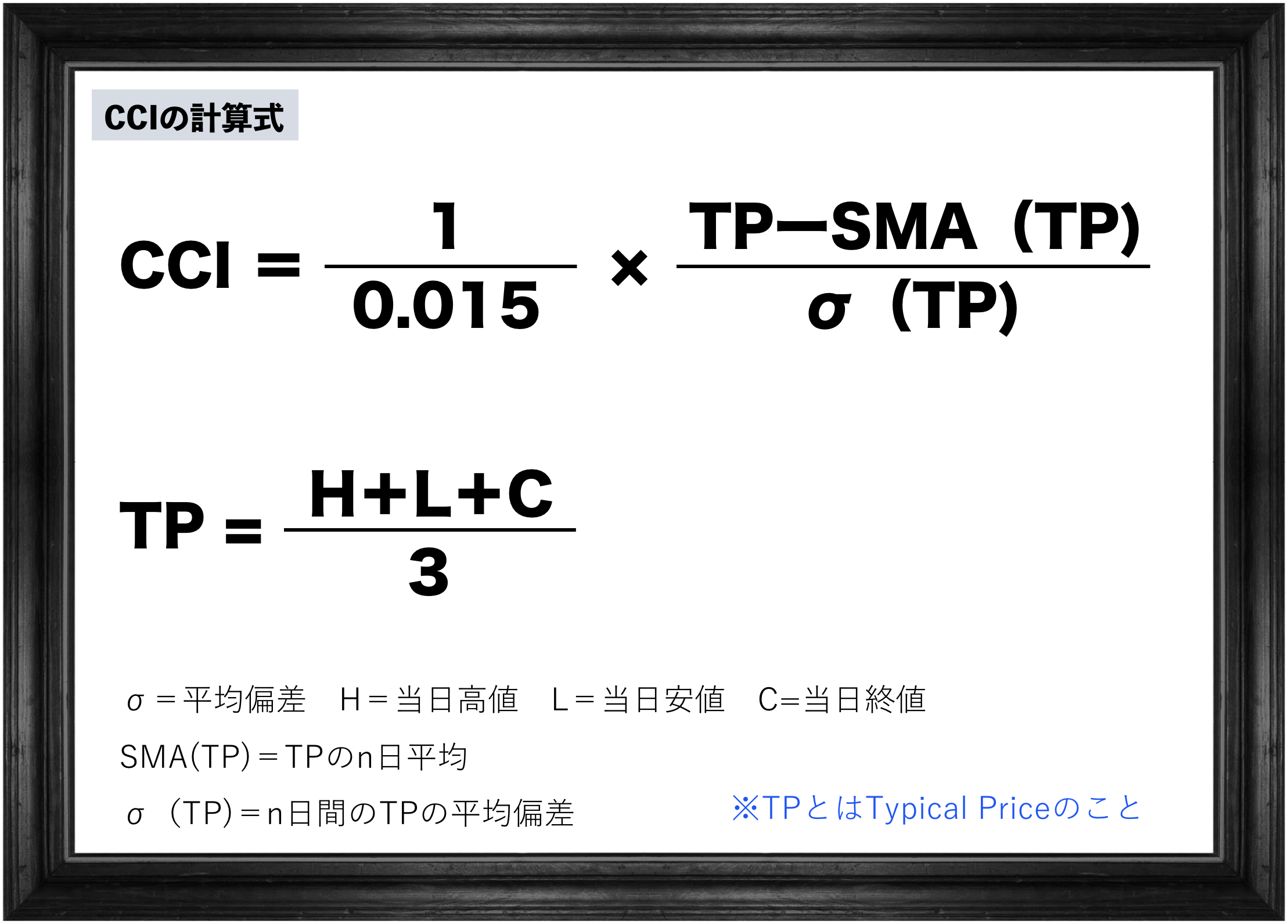

おぎゃー!!!!!
もう無理!!おうちに帰りたいぃぃぃ!!!
もう無理!!おうちに帰りたいぃぃぃ!!!

(さっきまでの頼もしさはどこへ………)

助けてぇぇ!!数字に殺される!!

これこれ。
お決まりのパターンで、数式見ただけで拒絶反応起こさないでください。それに謎のホームシックまで発症しちゃって…もう。
お決まりのパターンで、数式見ただけで拒絶反応起こさないでください。それに謎のホームシックまで発症しちゃって…もう。

だって、こんなの分かるわけないじゃないっすか!
読者の皆さんだってそう思ってますよ!
読者の皆さんだってそう思ってますよ!

どく…しゃ?

今はそこトボけなくていいっすよ…!

“分かるわけない”なんて、そんなことありませんよ。
それを分かりやすく教えるために私がいるんですから。
それを分かりやすく教えるために私がいるんですから。

ほ、ほ、ほ、ホントに!?!?

今までだってそうだったでしょう。
まぁでも、確かにこの式を見ただけじゃ
なんのことかチンプンカンプンですよね。
まぁでも、確かにこの式を見ただけじゃ
なんのことかチンプンカンプンですよね。

TPとかなんやねんホンマ…エグいわ……

この式はこういうものだったとひとまず置いておいて、
計算式の意味から紐解いていきましょうか。
計算式の意味から紐解いていきましょうか。
CCIの計算式の意味

時に瞬くん、別の指標で「移動平均線乖離率」というものは
ご存知ですか??
ご存知ですか??

移動平均線乖離率…?
いえ、知らないですけど名前からはなんとなく想像がつきます。
移動平均線と今の価格がどれくらい離れてるかを見るもの、とかですか?
いえ、知らないですけど名前からはなんとなく想像がつきます。
移動平均線と今の価格がどれくらい離れてるかを見るもの、とかですか?

そうです!名前からして分かりやすいですもんね。
基本的に価格と移動平均線の関係は、一緒に上昇し、一緒に下落する。
ですので、時にその間隔が離れ過ぎたとしてもやがて修正されてくるという考え方で成り立つもの。
基本的に価格と移動平均線の関係は、一緒に上昇し、一緒に下落する。
ですので、時にその間隔が離れ過ぎたとしてもやがて修正されてくるという考え方で成り立つもの。

その寄り戻しのところを狙っていくんですね。

どちらかと言うと、
トレンドの発生や終了を予兆してくれるもの、という考え方ですね。
例えば20日間なら
トレンドの発生や終了を予兆してくれるもの、という考え方ですね。
例えば20日間なら


というシンプルな計算式で、
仮に現在の価格1000円、20日の移動平均の値が900円だったら
(1000−900)÷900=0.111111…
で、今は約11%平均値と離れて価格が上にあるんだなぁ、ということが分かります。
仮に現在の価格1000円、20日の移動平均の値が900円だったら
(1000−900)÷900=0.111111…
で、今は約11%平均値と離れて価格が上にあるんだなぁ、ということが分かります。

単純明快っす。

ちなみに、このテクニカル指標の買いサイン・売りサインは小次郎講師流で言えば
・下降していた乖離線が底を打って上げ出したら買いサイン
・上昇していた乖離線が天井を打って下げ出したら売りサイン
となります。
まぁかなりザックリ目の指標ですが。
・下降していた乖離線が底を打って上げ出したら買いサイン
・上昇していた乖離線が天井を打って下げ出したら売りサイン
となります。
まぁかなりザックリ目の指標ですが。
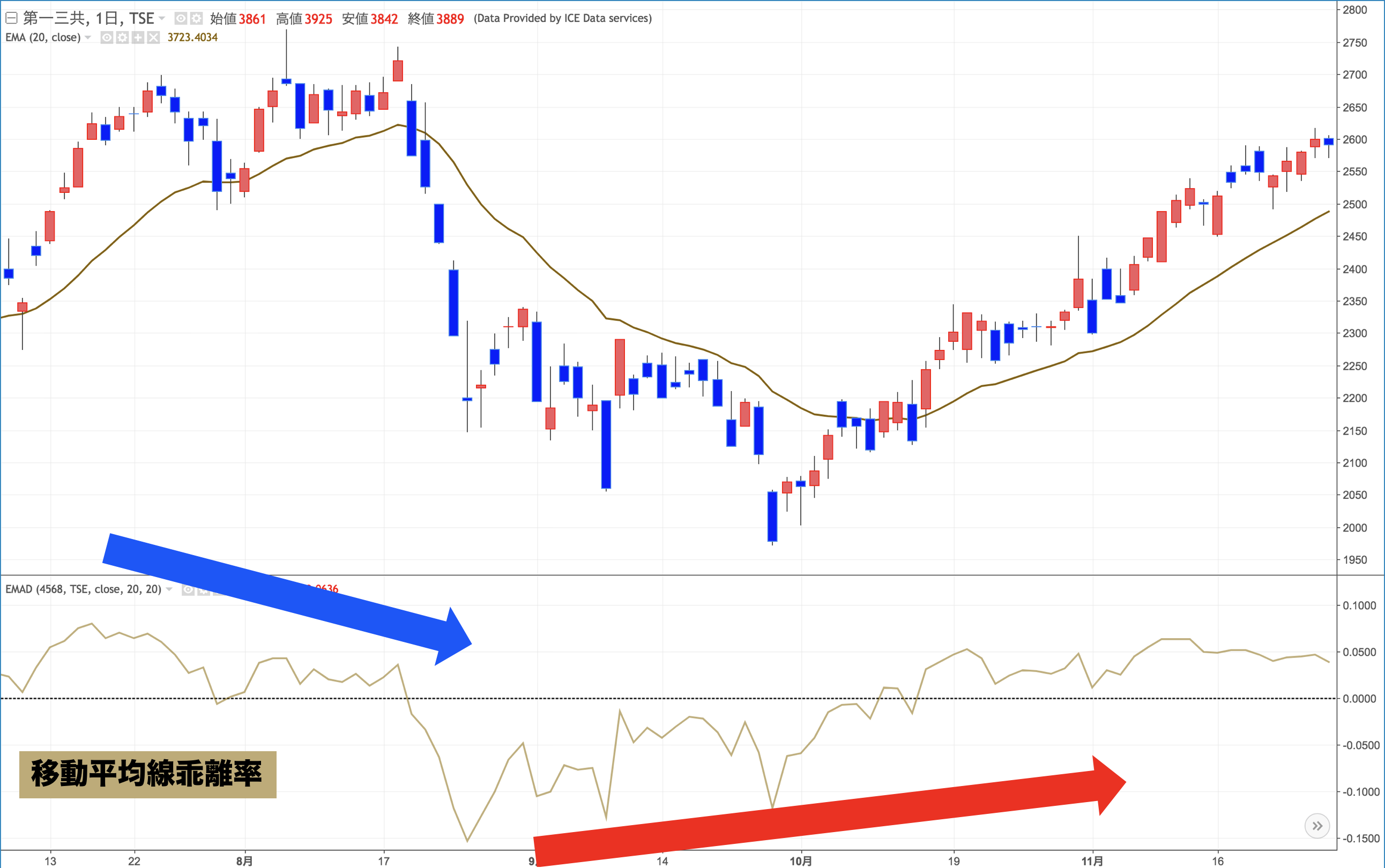

トレンドが勢いを失くして移動平均線が価格に近付いて来たら(乖離が解消されて来たら)、普通「あぁ、そろそろこのトレンドも終わりかな」と思いますもんね。

ただし!
何%乖離したらその後修正してくる、という明確な数値はないので、
「〇〇%以上離れたら反動が来る、つまり〇〇%下に離れたら買い、〇〇%上に離れたら売り」なんて書かれた本があったら、それは眉唾物なので騙されないように注意。
何%乖離したらその後修正してくる、という明確な数値はないので、
「〇〇%以上離れたら反動が来る、つまり〇〇%下に離れたら買い、〇〇%上に離れたら売り」なんて書かれた本があったら、それは眉唾物なので騙されないように注意。

りょ、了解っす!気をつけます。
にしても、師匠。この分かりやすい「移動平均線乖離率」とCCIの話がどうやって繋がるんですか??
にしても、師匠。この分かりやすい「移動平均線乖離率」とCCIの話がどうやって繋がるんですか??

結論から言うと
CCIはこの「移動平均線乖離率」の親戚!
CCIはこの「移動平均線乖離率」の親戚!

えぇっ!こんなシンプルな乖離率さんと親戚とはとても思えないっすよ!!

乖離率に失礼ですよ!
シンプルなものが悪いなんてことは全くありません。
真実というものは突き詰めれば往々に”シンプルな”答えに辿り着くのです。
シンプルなものが悪いなんてことは全くありません。
真実というものは突き詰めれば往々に”シンプルな”答えに辿り着くのです。

どこがどう似てるんだろうか…

まずは、この「移動平均線乖離率」と「CCI」が近しい考え方で出来ているということを頭に入れてもらって、次に進みましょう。
【TP】=【Typical Price】?

ではもう一度CCIの計算式のこの部分を見てください。
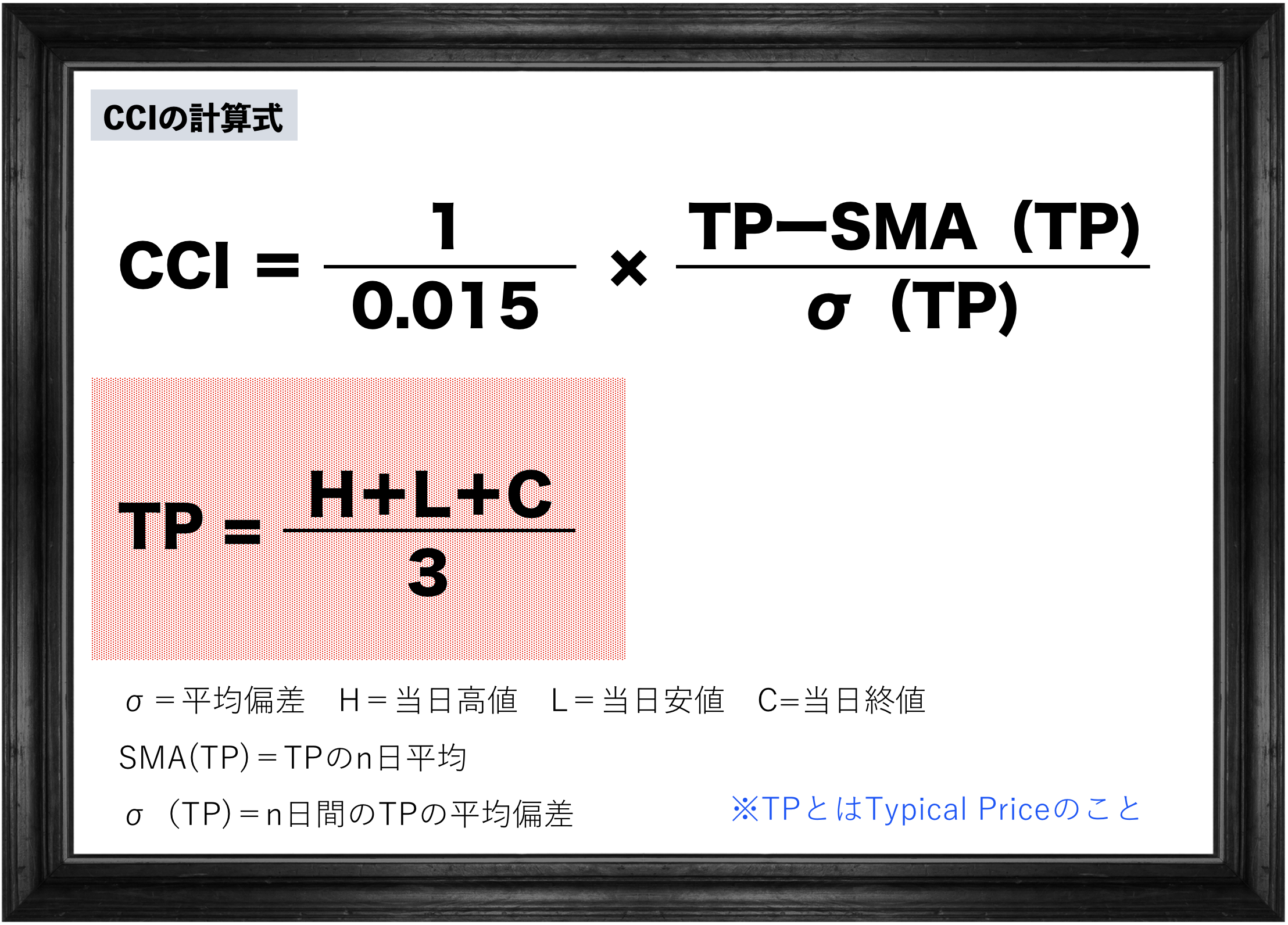

さっき瞬くんが「エグいわぁ…」とかエセ関西弁で言っていたように
この「TP」のアルファベットがまず分かりにくい原因ですよね。
この「TP」のアルファベットがまず分かりにくい原因ですよね。

(き、聞いてたんだ…恥ずかしい…)

このTPは「Typical Price」の頭文字で、
直訳すると「代表的な価格」という意味。
何が代表的かというと「高値と安値と終値の平均値」ということ。
直訳すると「代表的な価格」という意味。
何が代表的かというと「高値と安値と終値の平均値」ということ。

それを代表的な価格と呼ぶんですか?

実はテクニカル指標に使う価格というのはいくつか種類があるんです。
TPもその1つ。
通常よく使うのは「終値」ですよね?
TPもその1つ。
通常よく使うのは「終値」ですよね?

そうですね。移動平均線も高値とか安値じゃなく、終値の平均値ですもんね。

しかし、終値をその日の価格の”代表”と言っていいかどうかには
異を唱える声もあります。
異を唱える声もあります。

そんな声が!?

考えてもみてください。
終値をそもそも採用するというのは、それが一番直近の価格だからです。
だからそれが今現在の状況に一番近いだろうということでよく使われるんですが、じゃあそのロウソク足でものすごい高値を付けて終値は結構下がったね、という時に、その一瞬でも付けた高値を無視していいかと言われたら、決してそうじゃない。
終値をそもそも採用するというのは、それが一番直近の価格だからです。
だからそれが今現在の状況に一番近いだろうということでよく使われるんですが、じゃあそのロウソク足でものすごい高値を付けて終値は結構下がったね、という時に、その一瞬でも付けた高値を無視していいかと言われたら、決してそうじゃない。

そう言われると”代表”とは言い難いかも…

その日1日価格がずっと動かなかったのに、
立会終了ギリギリに突然価格が上昇し出して、
終値だけ異常に高いとか、逆に終値だけ異常に安いなんてことも時にはあり得ますよね?
立会終了ギリギリに突然価格が上昇し出して、
終値だけ異常に高いとか、逆に終値だけ異常に安いなんてことも時にはあり得ますよね?

それはあり得ますね。

だから、終値だけよりも1日に付けた価格それぞれの平均値の方が、
テクニカル指標の計算に適しているんじゃないかという考え方もあるんです。
テクニカル指標の計算に適しているんじゃないかという考え方もあるんです。
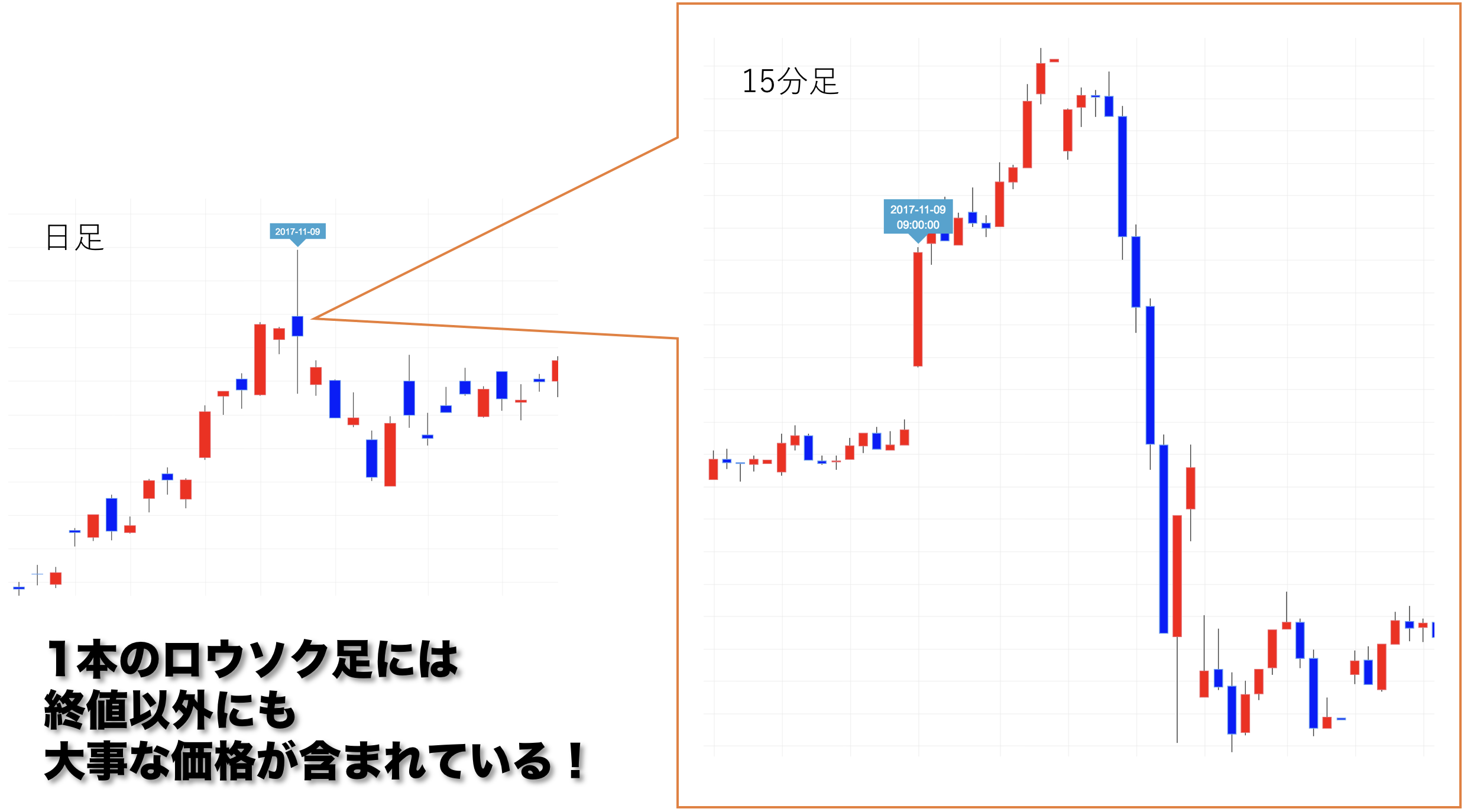

なるほど。終値だけが全てじゃないんですね。

テクニカル指標に使われる本日の価格には、主に次の種類があります。
あくまで参考と言ったところですが。
あくまで参考と言ったところですが。


終値を採用するパターンしか知らなかった…!

どれが良いとか、どれが一番正確か、という問題ではなく、
それぞれに特徴があるということなんですね。
それぞれに特徴があるということなんですね。

そしてCCIを発明したランバートさんは高値と安値と終値を3で割った代表値の【TP】を使いたいんだ、と。

そう、あくまでそういうことなんです。

こうやって見るとCCIの式の下半分は攻略したも同然っすね。
TPはただの代表値ですし。
TPはただの代表値ですし。
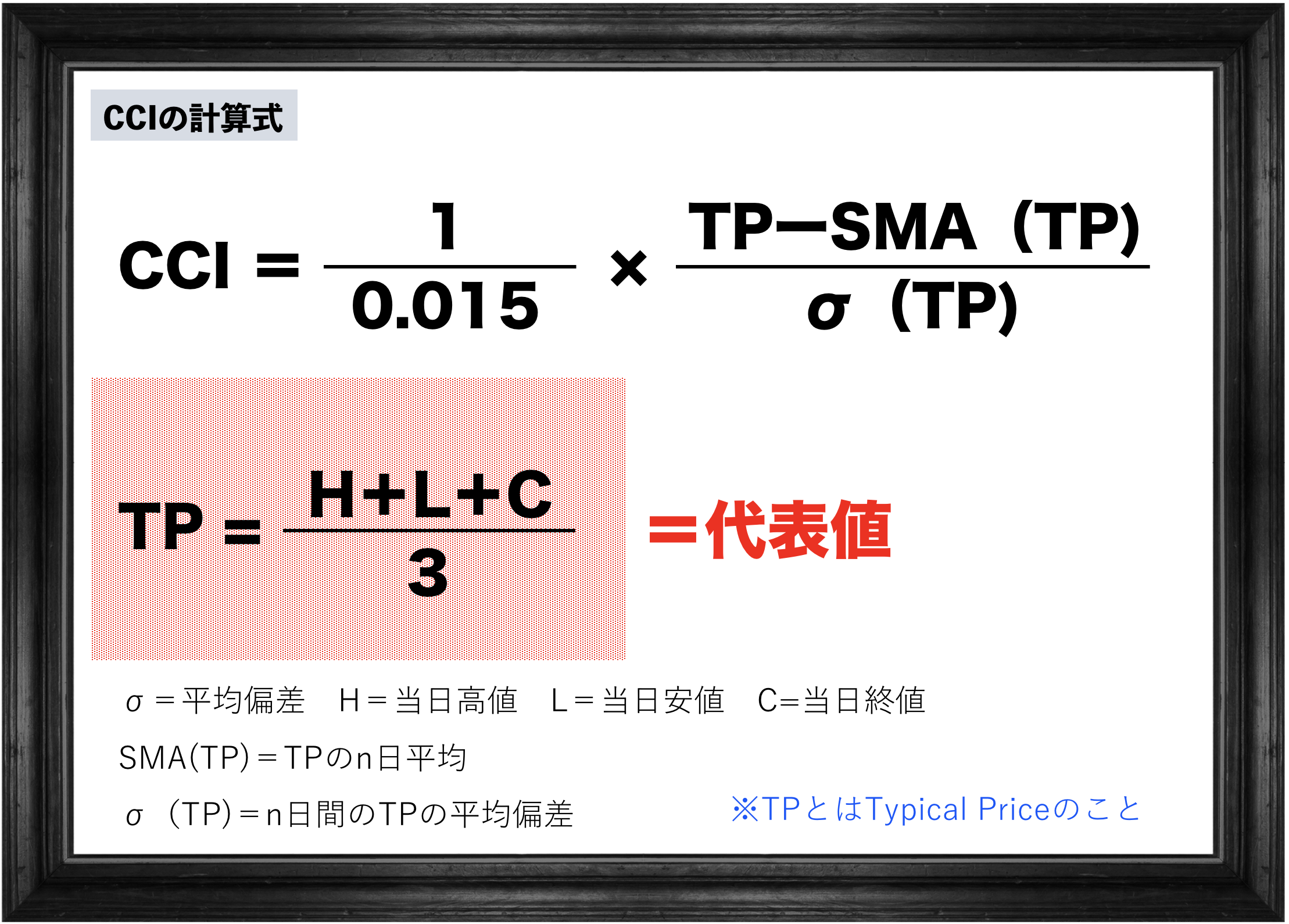

いえいえ、もっと攻略してますよ!

えぇっ!?

式の右上にも注目してください。
この部分、今まで話したことの何かに似てませんか…?
この部分、今まで話したことの何かに似てませんか…?

分母の「σ」はよくわからないから置いといて…
えーと…
あ!!上で見た「移動平均線乖離率」の計算式とそっくりだ!
えーと…
あ!!上で見た「移動平均線乖離率」の計算式とそっくりだ!

お見事!
代表値と終値の違いこそありますが、この部分は乖離率の計算式が分かればあら不思議、途端に理解できる部分となるのです!!
代表値と終値の違いこそありますが、この部分は乖離率の計算式が分かればあら不思議、途端に理解できる部分となるのです!!


並べてみると分かりやすいですねぇ。

親戚といった意味が分かったでしょう?
実際にチャートで同時に表示してみても、似たような動きをしています。
実際にチャートで同時に表示してみても、似たような動きをしています。
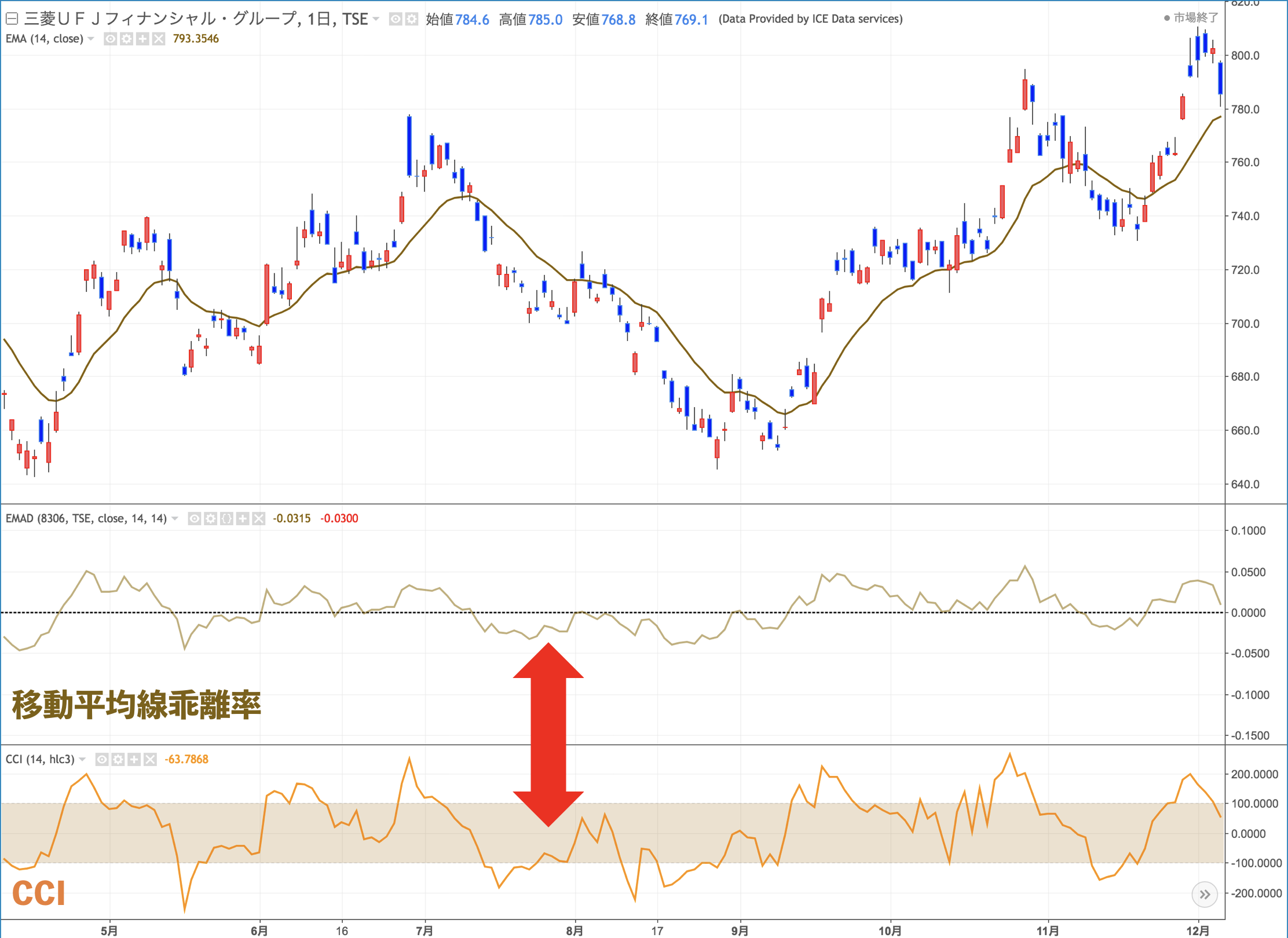

ホントそうですね。
細かい部分は抜きにして、大まかな動きは一緒です。
細かい部分は抜きにして、大まかな動きは一緒です。

つまりCCIは移動平均線乖離率の変化ver.。
そしてこの「n日移動平均」の日数によく使われるパラメーターは14。
そしてこの「n日移動平均」の日数によく使われるパラメーターは14。

RSIにも使われてた数字だ!

あの有名なテクニカルアナリストのワイルダーさんが好んで使った数字ですね。やはり有用な数値には普遍性があるんですよ。
とすると、後はこの「σ」と式の左側の意味さえ分かれば
CCIの計算式は使えるようになりますね。
とすると、後はこの「σ」と式の左側の意味さえ分かれば
CCIの計算式は使えるようになりますね。

しかし残念ながら良いところで、後半へ続く。

一回じゃ全部頭に入んないすからね…!次回に期待。
それにしても、この果樹園の地図記号みたいな「σ」は何なんですか?
それにしても、この果樹園の地図記号みたいな「σ」は何なんですか?

え!?果樹園のマークはこれでしょう!


…と出してみたら意外と……似てるッッ!!

ほら!ですよね!?
あぁ。僕の好きな「梨」のこと考えたらまたヨダレが…
あぁ。僕の好きな「梨」のこと考えたらまたヨダレが…

本当に食いしん坊だな!!

ちなみに僕の地元は梨の産地なんですけど、
家の近くにある厳しめの進学校(?)の校則に「近隣の梨園に無断で立ち入ったら停学、梨を捥いだら退学」なんてのがあるとかないとか…
家の近くにある厳しめの進学校(?)の校則に「近隣の梨園に無断で立ち入ったら停学、梨を捥いだら退学」なんてのがあるとかないとか…

梨で一発レッド!?
それこそ眉唾物ですねぇ…
それこそ眉唾物ですねぇ…
おしまい